
Hình sao năm cánh là một trong những hình thú vị nhất trong hình học. Những môn đồ của Pythagoras thậm chí còn lấy nó làm biểu tượng của mình. Hình sao năm cánh đều có chứa tỉ lệ vàng (sẽ đề cập đến kĩ hơn ở phần sau) và xuất hiện tới 50 lần trên lá quốc kì của nước Mĩ!
Chúng ta đều biết rằng tổng ba góc của một tam giác bằng 180° và tổng bốn góc của một tứ giác bằng 360°. Thế còn tổng các góc của một hình sao năm cánh thì sao? Tính chất này rất dễ chứng minh, nhưng ta sẽ thừa nhận rằng tất cả các hình sao năm cánh đều có tổng số đo các góc bằng nhau. Như vậy, ta có thể tìm tổng các góc của hình sao năm cánh đều và tổng quát hóa cho tất cả các hình sao năm cánh khác. Bạn chỉ cần tìm ra số đo của một góc là sẽ tính được tổng số đo các góc. Điều này không khó vì cả năm góc đều bằng nhau và hình sao năm cánh đều rất đối xứng.
Tuy nhiên, giả sử chúng ta không suy luận ra điều này và chỉ chú tâm đến việc tìm tổng số đo các góc của một hình sao năm cánh “méo mó” được vẽ tùy ý như hình sau:
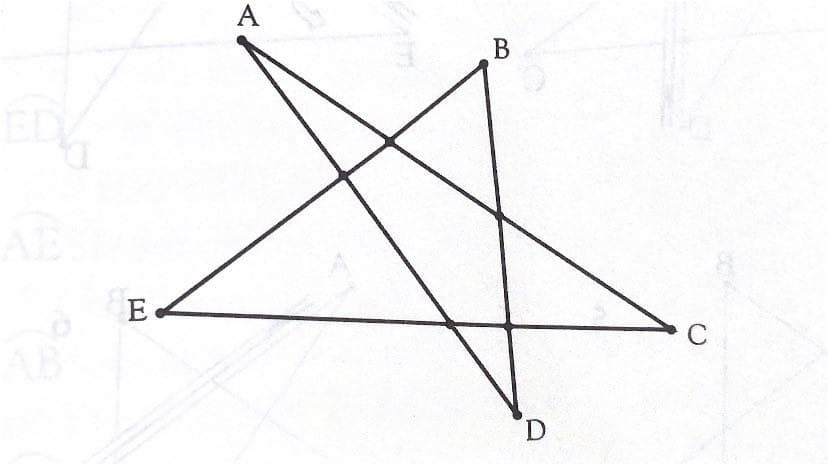
Ta có thể xác định được tổng các góc bằng cách đặt một chiếc bút chì lên đoạn AC sao cho đầu bút chỉ vào điểm A. Quay chiếc bút theo góc A cho đến khi chiếc bút nằm trên đoạn AD (đầu bút chỉ vào A). Quay theo góc D cho đến khi bút trùng với đoạn BD và đầu bút chỉ vào B. Quay theo góc B cho đến khi chiếc bút nằm trên BE, đầu bút chỉ vào B. Quay bút theo góc cho đến khi bút trùng với đoạn EC, đầu bút chỉ vào C. Cuối cùng, quay bút theo góc C cho đến khi bút nằm trên đoạn AC, đầu bút chỉ vào C, tức là ngược lại với trạng thái ban đầu của bút. Như vậy, chiếc bút chì đã đảo ngược chiều, tức là quay một góc 180°, suy ra tổng các góc của hình sao năm cánh (những góc mà đầu bút chì lần lượt quay quanh) cũng là 180°.
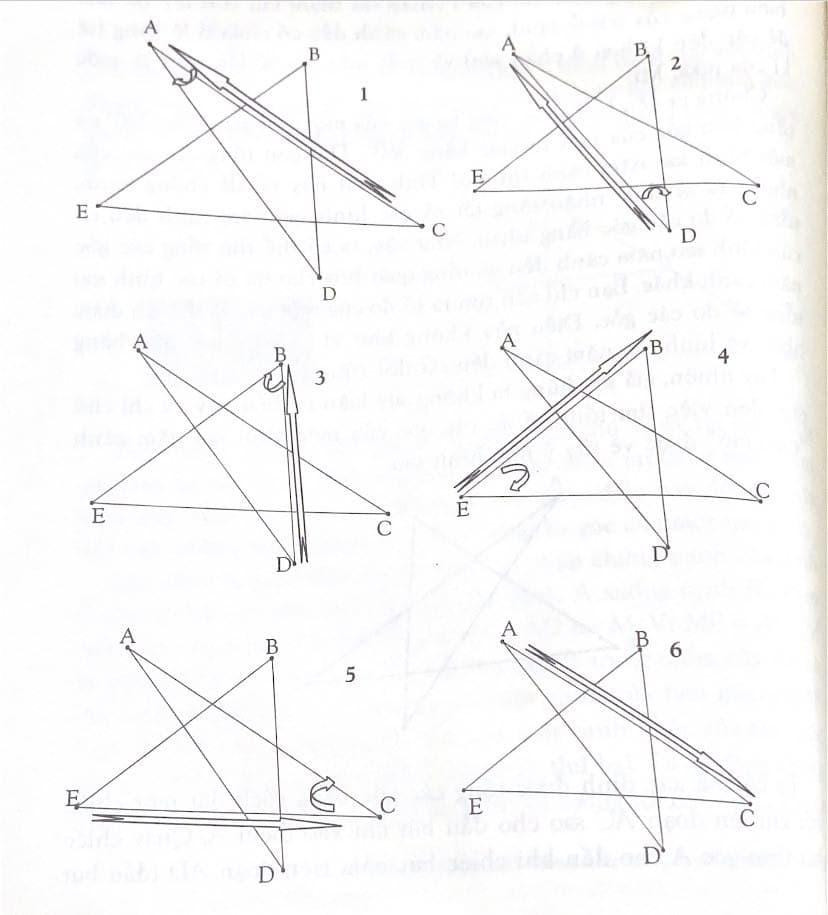
Một lần nữa, các bạn hãy chú ý hướng của bút chì thay đổi 180 khi ta quay bút một vòng quanh các góc.
Dưới đây, chúng tôi xin trình bày một phép “chứng minh" bằng hình học cho những bạn đọc quan tâm. Lưu ý rằng chúng ta thừa nhận tổng năm góc của tất cả các hình sao năm cánh đều như nhau. Vì ta được phép chọn một hình sao năm cánh bất kì nên ta có thể lấy một hình sao năm cánh đều hoặc hình sao năm cánh nội tiếp trong một đường tròn (cả năm đỉnh của hình đều nằm trên một đường tròn). Trong cả hai trường hợp này, ta nhận thấy mỗi góc của hình sao năm cánh đều là một góc nội tiếp của đường tròn nên có số đo bằng một nửa số đo của cung bị chắn (1)
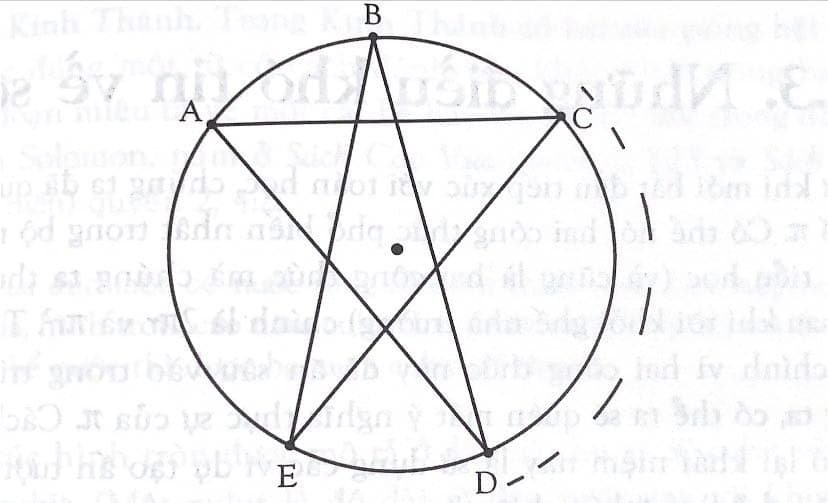
Như vậy, ta có:
\(\widehat{A}\) = 1/2 \(\widehat{CD}\) (" góc A có số đo bằng một phần hai số đo của cung \(\widehat{CD}\)")
\(\widehat{B}\) = 1/2 \(\widehat{ED}\)
\(\widehat{C}\) = 1/2 \(\widehat{AE}\)
\(\widehat{D}\) = 1/2 \(\widehat{AB}\)
\(\widehat{E}\) = 1/2 \(\widehat{BC}\)
Nếu cộng từng vế các phương trình trên lại với nhau, ta có:
\(\widehat{A}\) + \(\widehat{B}\) + \(\widehat{C}\) + \(\widehat{D}\) + \(\widehat{E}\) = 1/2 (\(\widehat{CD}\) + \(\widehat{ED}\) + \(\widehat{AE}\) + \(\widehat{AB}\) + \(\widehat{BC}\)) = 1/2 X \(360^0\)
Như vậy, tổng các góc của một hình sao năm cánh bằng một phần hai số đo độ của một đường tròn, tức là bằng 180°. Xin nhắc lại rằng chứng minh của chúng ta không mất đi tính tổng quát khi ta chọn một điều kiện thích hợp hơn cho hình sao năm cánh. Nói cách khác, ta có thể thay đổi hình vẽ sao cho dễ tính toán hơn mà vẫn không làm mất đi tính tổng quát của bài toán.
(1). Góc nội tiếp của một đường tròn là góc có đỉnh nằm trên đường tròn đó. Cung bị chắn của một đường tròn là cung bị "giới hạn" bởi các tia của một góc. Góc nội tiếp có số đo bằng một phần hai số đo của cung bị nó chắn.
Nguồn: VẺ ĐẸP TOÁN HỌC
Mathchallenge.vn