Để nhận thức đúng hơn về sức mạnh của các định lí (hoặc tính chất) trong hình học, bạn hãy thử vẽ một số hình tứ giác thật “méo mó” (hình dáng nào cũng được). Sau đó, xác định (thật cẩn thận) trung điểm bốn cạnh của mỗi hình tứ giác mà bạn vừa vẽ. Nếu bạn liên tiếp nối các trung điểm này với nhau, bạn sẽ thu được một hình bình hành. Thật bất ngờ! Vì sao lại có điều này? Các hình tứ giác mà bạn vẽ có lẽ đều có hình dáng khác nhau, vậy mà cuối cùng ta lại thu được một hình bình hành bên trong tất cả các hình ban đầu.

Dưới đây là một vài ví dụ:

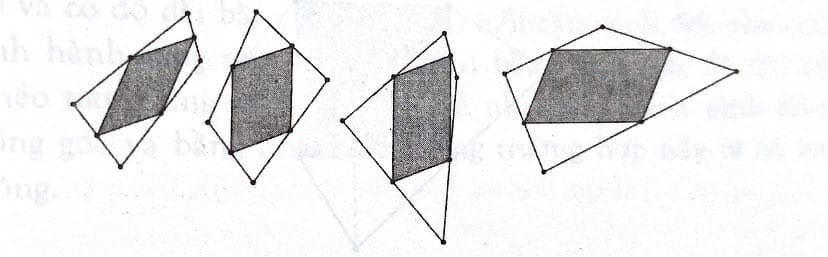
Câu hỏi đặt ra ở đây là cần vẽ hình tứ giác ban đầu như thế nào để hình bình hành tạo ra từ bốn trung điểm của bốn cạnh tứ giác là hình chữ nhật, hình thoi hoặc hình vuông?

Bạn có thể đoán mò rồi thử lai, hoặc cũng có thể phân tích bài toán để thu được kết quả sau:

Khi hai đường chéo của hình tứ giác ban đầu vuông góc với nhau, hình bình hành thu được sẽ là hình chữ nhật.

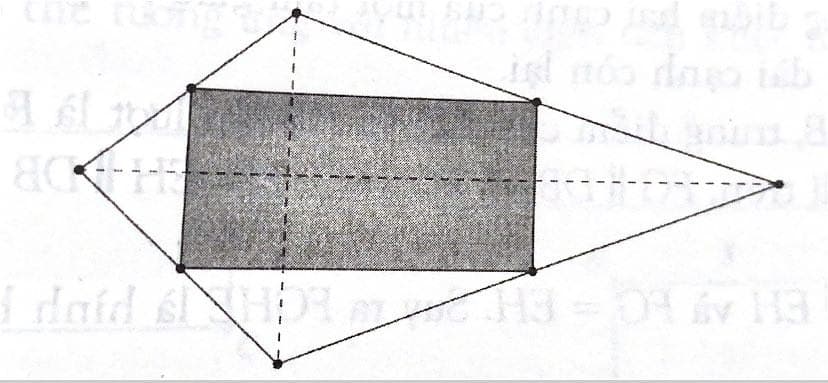
Khi hai đường chéo của hình tứ giác ban đầu bằng nhau, hình bình hành thu được sẽ là hình thoi.

Khi hai đường chéo của hình tứ giác ban đầu bằng nhau và vuông góc với nhau, hinhg bình hành thu được sẽ là hình vuông.

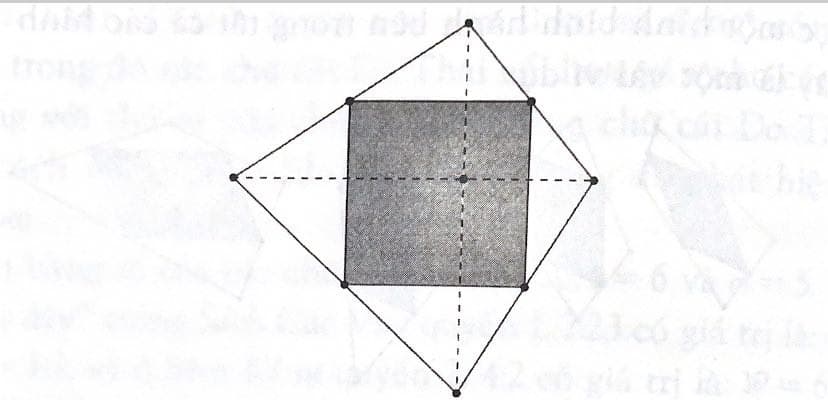
Những bạn đọc quan tâm muốn tìm hiểu sâu hơn có thể sử dụng phần mềm Geometer's Sketchpad. Đối với những bạn muốn chứng minh tất cả những điều trên “thực sự đúng", chúng tôi xin trình bày qua một cách chứng minh đơn giản hoàn toàn nằm trong khả năng của các bạn học sinh phổ thông.

Tóm tắt cách chứng minh:

Cách chứng minh này dựa trên một định lí rất đơn giản: đường thẳng nối trung điểm hai cạnh của một tam giác song song và có độ

dài bằng ½ độ dài cạnh còn lại. Trong tm giác ADB, trung điểm của AD và AB lần lượt là F và G.

Theo định lí trên, FG || DB và FG = 1/2 BD, EH || DB và EH =1/2 BD.

Do đó, FG || EH và FG = EH. Suy ra FGHE là hình bình hành.

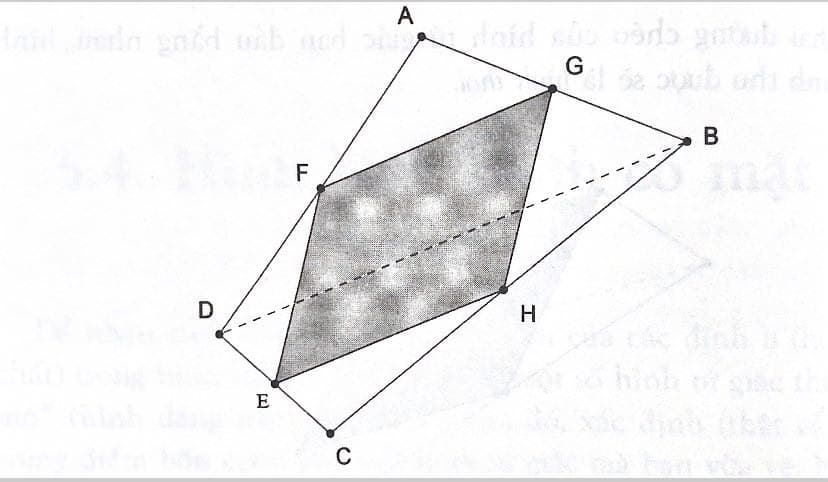
Hơn nữa, nếu hai đường chéo BD VÀ AC bằng nhau thì các cạnh của hình bình hành cũng bằng nhau vì các cạnh này đều bằng một nửa độ dài các đường chéo của hình tứ giác ban đầu. Do đó, ta có một hình thoi.

Tương tự, nếu hai đường chéo của hình tứ giác ban đầu vuông góc với nhau và có độ dài bằng nhau, thì do mỗi cặp cạnh đối nhau của hình bình hành song song và có độ dài bằng một nửa độ dài của đường chéo tương ứng nên các cạnh kề nhau của hình bình hành phải vuông góc và bằng nhau. Vậy trong trường hợp này ta có một hình vuông.

Nguồn: VẺ ĐẸP TOÁN HỌC

mathchallenge.vn